[Anuvaad lambit hai]
[Devanaagaree mein upalabdh hai: मिस्री-ज्ञान-केंद्र.भारत]

I parametri del progetto armonico

 

Il design armonico nell'architettura dell'antico Egitto è stato ottenuto attraverso l'unificazione di due sistemi:

1. Aritmetica (numeri significativi).

2. Grafica (quadrati, rettangoli e alcuni triangoli).

L'unione dei due sistemi riflette la relazione delle parti con il tutto, che è l'essenza del design armonico.

Questa unione di aritmetica e progettazione grafica segue gli elementi descritti di seguito.

 

1. Il sistema aritmetico era composto da:

1-a. Gli assi attivi

Un asse è una linea immaginaria e ideale attorno alla quale ruota un corpo in movimento. In geometria, un asse è altrettanto immaginario: una linea senza spessore.

Il tempio egizio era considerato un'unità organica e vivente. È in costante movimento; i suoi intricati allineamenti e le sue molteplici asimmetrie lo fanno oscillare attorno ai suoi assi. Questo movimento avviene all'interno di un ritmo dato dal “modulo” o dal coefficiente particolare della cosa o dell'idea da definire.

Il design architettonico dell'antico Egitto si distingue per la sua forte simmetria apparente attorno ad un asse longitudinale. Questo è il risultato della conoscenza dell'Antico Egitto delle leggi cosmiche. Il designer egiziano ha rispecchiato questa lieve asimmetria cosmica assicurandosi che gli elementi su entrambi i lati dell’asse non fossero esattamente identici tra loro. Sebbene la maggior parte di essi siano equilibrati, gli elementi non sono simmetrici. Di seguito sono mostrati due esempi di assi definiti nei disegni dell'antico Egitto.

La linea dell'asse è rinvenibile in alcuni disegni architettonici recuperati o in schizzi su papiri e tavolette di varie epoche. Si trattava presumibilmente di annotazioni operaie e, nonostante il loro scopo pratico, presentano ancora la linea dell'asse tracciata nello stesso modo convenzionale dei disegni moderni.

Negli edifici stessi l'asse è segnato da una linea incisa sulle pietre del corso superiore di una lastra di fondazione, come nel caso del Tempio di Luxor.

1-b. Punti significativi (lungo l'asse)

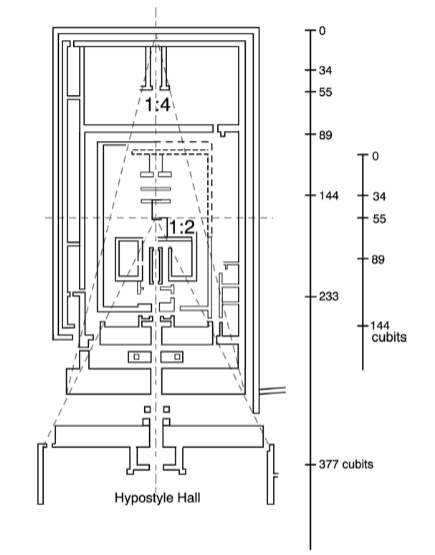
I punti significativi sono stati determinati lungo l'asse di progettazione. Questi punti segnano l'intersezione con assi trasversali, l'allineamento di una porta centrale, la posizione di un altare, il centro del santuario, ecc. Questi punti significativi seguono una precisa progressione aritmetica. In molti dei migliori piani, questi punti significativi sono a distanze armoniche l'uno dall'altro, e le loro distanze da un'estremità all'altra esprimono le figure della Serie Sommatoria (la cosiddetta Fibonacci), 3, 5, 8, 13, 21 , 34, 55, 89, 144, 233, 377, 610, . . . L'analisi armonica mostra una serie di punti significativi leggibili da entrambe le estremità, ovvero se invertito, un sistema di punti significativi corrisponderebbe anche alla Serie con il punto di riferimento che inizia all'estremità opposta del piano.

Alti numeri della Serie della Sommazione furono cristallizzati nei monumenti egiziani fin dall'Antico Regno. Il disegno del tempio piramidale di Khafra (Chephren) raggiunge la cifra di 233 cubiti nella sua lunghezza totale, misurata dalla piramide, con una serie completa di DIECI punti significativi.

Il Tempio di Karnak segue le cifre della Serie delle Sommazioni fino a 610 cubiti, cioè DODICI punti significativi. [Vedi i diagrammi di entrambi i templi nel prossimo capitolo].

 

2. Il sistema grafico era composto da:

2-a. I triangoli telescopici

La tipica pianta del tempio egizio aumenta in larghezza e altezza dal santuario verso la parte anteriore. Questa delimitazione complessiva si basava su un "sistema telescopico" di progettazione fin dall'Antico Regno. L'aumento della larghezza è stato ottenuto mediante l'uso di triangoli consecutivi 1:2, 1:4 e 1:8 da uno o più punti significativi. [Vedi il diagramma del Tempio di Karnak (parziale) di seguito.]

 

La stessa configurazione telescopica si applicava al piano verticale, per cui il pavimento del tempio scendeva e i tetti salivano verso l'esterno verso i piloni del tempio; come mostrato in diversi templi in un capitolo precedente di questo libro.

2-b. I perimetri rettangolari

Gli schemi generali orizzontali e verticali sono sostanzialmente di forma rettangolare, sia per la pianta complessiva che per le sue parti costitutive. Le configurazioni più comuni utilizzate sono:

• Un quadrato semplice, come quello utilizzato nel Tempio Piramide di Khafra (Chephren) a Giza.

• Un doppio quadrato o rettangolo 1:2, come il Complesso Zoser a Saqqara, il recinto interno a Karnak e la sala delle feste di Twt Homosis III

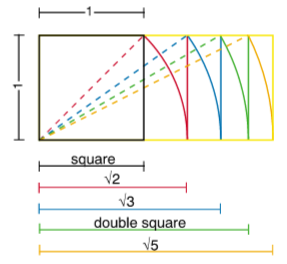
• Rettangoli radice: numerosi esempi [mostrati di seguito].

 

• Il rettangolo Neb (d'oro), dove il "valore numerico" del rapporto tra i due lati è pari a 1,618: numerosi esempi come nel Tempio Piramide di Khafra a Giza [mostrato in precedenza].

 

Il piano verticale

Gli antichi egizi erano maestri del principio verticale così come della linea orizzontale. Le altezze verticali seguivano lo stesso aumento proporzionale delle larghezze orizzontali man mano che venivano apportate aggiunte alla facciata dei monumenti, un aspetto caratteristico dei templi egiziani.

La proporzione armonica veniva applicata dagli antichi egizi in tutte e tre le dimensioni, come ad esempio:

• Le piramidi (basi quadrate e volume triangolare).

• Il caso eclatante della Sala del Re nella Piramide di Khufu (Cheope), che offre relazioni esatte per la grande diagonale nello spazio rispetto alla dimensione del lato. [Vedere il diagramma nel capitolo 11.]

• Piloni. [Vedere il diagramma nel capitolo 11.]

• Porte/portali/cancelli. [Vedere il diagramma nel capitolo 11.]

• Le altezze verticali seguivano lo stesso aumento proporzionale delle larghezze orizzontali, poiché venivano apportate aggiunte alla parte anteriore dei monumenti, un aspetto caratteristico dei templi egizi.

Varie applicazioni del design armonico nelle opere dell'Antico Egitto nel corso della sua storia recuperata - e in tutto il paese - si trovano nel prossimo capitolo di questo libro.

 

[Un estratto da L'architettura metafisica dell'antico Egitto di Moustafa Gadalla]