Le cycle des quintes et l'unité de mesure musicale égyptienne

 

1. Panta (Tous) est un dérivé de Pente (Cinq)

Les anciens Égyptiens exprimaient leur connaissance de tous les sujets sous forme d’histoires, comme l’ont noté tous les premiers historiens grecs et romains. L’histoire d’Isis et d’Osiris était le modèle égyptien utilisé pour expliquer toutes les facettes de la connaissance.

Le rôle d'Isis et d'Osiris, en ce qui concerne les trois saisons rythmiques égyptiennes, est mieux décrit dans Diodore de Sicile [Livre I, 11. 5-6]:

Ces deux neteru (dieux), qu'ils détiennent, régulent l'univers entier, donnant à la fois nourriture et croissance à toutes choses au moyen d'un système de trois saisons qui complètent le cycle complet par un mouvement inobservable. . . et ces saisons, bien que dans la nature les plus opposées les unes aux autres, complètent le cycle de l'année dans la plus complète harmonie.

Pour les Égyptiens, Isis et Osiris régulaient la musique des sphères. Les harmonies universelles se jouent entre ces deux symboles universels primitifs masculins et féminins d'Isis et d'Osiris, dont le mariage céleste a produit le fils Horus.

Plutarque a écrit sur la signification numérique de la triade égyptienne Isis, Osiris et Horus dans Moralia Vol. V que les anciens Égyptiens assimilaient le nombre deux à Isis, trois à Osiris et cinq à Horus.

Trois (Osiris) est le premier nombre impair parfait : quatre est un carré dont le côté est le nombre pair deux (Isis) ; mais cinq (Horus) est à certains égards semblable à son père, et à certains égards à sa mère, étant composé de trois et deux. Et panta (tout) est un dérivé de pente (cinq), et ils parlent de compter comme de « compter par cinq ».

La signification et la fonction du chiffre cinq, dans l’Égypte ancienne, sont indiquées par la manière dont il était écrit. Le nombre cinq dans l’Égypte ancienne s’écrivait sous la forme de deux II au-dessus de trois III (ou parfois sous la forme d’une étoile à cinq branches). En d’autres termes, le numéro cinq (le fils – Horus) est le résultat de la relation entre le numéro deux (la mère – Isis) et le numéro trois (le père – Osiris).

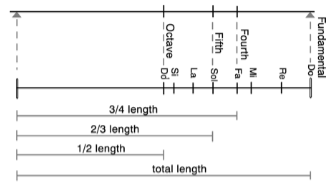
Musicalement, le rapport/rapport de 2:3 sur la corde vibrante et sur le clavier détermine la vibration de la Cinquième Parfaite, s'étendant sur cinq intervalles (comme indiqué ici).

Sur un monoaccord, le son de la quinte naturelle est produit lorsque la corde est maintenue enfoncée en un point qui divise la corde dans un rapport de 2:3 (comme illustré ci-dessus).

L'intervalle de la Quinte offre l'harmonie la plus forte possible entre deux tons différents. C'est le premier intervalle harmonique auquel se rapportent tous les autres intervalles harmoniques.

Plutarque a souligné l'importance de la Cinquième pour les Égyptiens, dans son Moralia Vol. V:

Et panta (tout) est un dérivé de pente (cinq), et ils [les Égyptiens] parlent de compter comme de « compter par cinq ».

 

2. Progression de la quinte harmonique

Les anciens Égyptiens comptaient « par cinq », et la progression la plus forte et la plus naturelle d’une harmonie à l’autre est le résultat d’un tel développement.

Toutes les gammes musicales sont générées par la progression de la Cinquième. La forme/relation de cette première consonance est la première Cinquième établie par le mariage céleste d'Isis et Osiris. Ils devenaient à leur tour un modèle à former, par une succession de relations similaires, selon une progression géométrique.

Les sept tons de la gamme diatonique (Faire, Ré, Mi, Fa, Sol, La, Si) sont le résultat de trois progressions de Quintes. Pour simplifier les choses, nous illustrerons les trois progressions de la Quinte au clavier, comme suit :

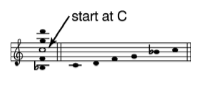
1. Si nous commençons par n'importe quelle note de musique, disons le milieu C (Do), en tant que générateur, puis trouvez ses deux quintes réciproques, comme indiqué ci-dessus (F et g):

2. La deuxième progression (de F et g) génère deux cinquièmes réciproques supplémentaires (B et D), des deux cinquièmes ci-dessus. Cela donne l’échelle pentatonique.

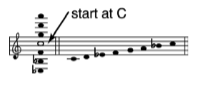
3. Troisième progression (de B et D) : en ajoutant deux quintes réciproques supplémentaires (E et UN), l'échelle heptatonique est obtenue.

L'échelle diatonique est ainsi formée de sept termes adjacents quelconques d'une série géométrique, régis par la constante 3/2 ou 2/3 – la proportion de la Cinquième Parfaite. Les sept tonalités musicales naturelles sont donc obtenues à partir de l'opération générative qui s'étend trois fois, mais pas plus.

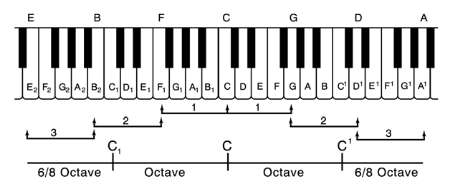
Pour illustrer le cycle des quintes consécutives, qui produisent la gamme diatonique sur le clavier, imaginons que les tons le long de la ligne supérieure (EBFCGDA) forment un cercle avec le ton C-le ton du générateur dans notre cas-en haut. Le résultat sera le diagramme commun connu sous le nom de Cycle/Cercle des Cinquièmes, comme indiqué ici. De la note C (Do), on progresse trois fois dans chaque sens, pour atteindre les sept tons de la gamme diatonique.

La progression harmonique le long du cycle des Quintes parfaites est la plus naturelle, et une succession d'harmonies qui ne sont pas dans ce rapport a le caractère d'un retard ou d'une suspension de cette progression naturelle. D'une seule Quinte donnée découle tout le système musical, qui doit naturellement être dans la même proportion que le premier. Il n’y a eu aucune modification de cette proportion ni substitution à une autre.

Comme indiqué précédemment, les Égyptiens comprenaient que le chiffre 2 (représenté par Isis) et le chiffre 3 (représenté par Osiris) régulaient l'univers entier, y compris la musique.

Toutes les relations d'intervalle peuvent être réduites à 3^X:2^oui ou 2^X:3^oui. Voici trois exemples pour illustrer un tel fait :

• Le ton parfait = 8:9 = 2³:3²
C’est aussi le rapport musical parfait, car c’est le rapport entre les réciproques de 2 et 3 à leurs puissances réciproques de 3 et 2.

• L'intervalle, reflux, tel que déterminé en termes de vibrations par seconde, est 65536/59049, ce qui équivaut à 2¹⁶/3¹⁰.

• L'intervalle, disons 384 cents, tel que déterminé par les vibrations par seconde, est 8 192/6 561 = 2.¹³/3⁸.

La progression par les quintes pour atteindre les sept tons de la gamme diatonique, comme illustré sur une illustration antérieure sous le clavier, nous montre que les quintes générées (auto-produites) ne coïncident jamais avec les octaves en progression.

Le clavier, cependant, ne peut pas nous donner la véritable représentation de la relation entre la progression des quintes et des octaves. Il faut donc suivre l'exemple montré sur l'illustration mono-accord précédente où il est montré que la Quinte Parfaite est produite par 2/3 de la longueur totale de la corde et l'octave à la ½ de sa longueur.

Une progression par Cinquièmes Parfaites signifiera trouver la Cinquième Parfaite suivante aux 2/3 des 2/3 d'origine de la longueur, etc. Il est facile de voir que tout progrès en Quintes signifie multiplier par le rapport 2:3 par lui-même, et aucune puissance de 3 ne peut jamais coïncider avec une puissance de 2, ce que requiert l'octave.

Nous continuons à nous développer par cinquièmes dans les deux sens (haut et bas de l'échelle). Les transpositions successives de la gamme produisent de nombreux dièses et bémols, disposés par quintes. Le cycle des Perfect Fifths autoproduits est tracé le long de sa longueur/circonférence : la corde est imaginée comme étant bouclée sous la forme d'un cercle.

Il a été constaté qu'après 53 quintes naturelles, toute nouvelle quinte coïncide opportunément avec une quinte existante antérieure. L'incrément entre les 53 quintes naturelles était/est appelé un virgule. Ainsi, les Égyptiens définissaient le système de tons, en référence au Cercle des Quintes, sur la base de l'unité de mesure connue sous le nom de virgule, en subdivisant l'octave en 53 pas égaux. Ce virgule a une valeur de 22,6415 cents. (UN cent est une unité standard pour mesurer les intervalles musicaux. Une octave équivaut à 1 200 cents.)

Il est intéressant de noter que les traités européens du Moyen Âge font référence à cette virgule particulière de 22,6415 centimes comme un « Virgule arabe », même si aucune documentation écrite arabe dans le monde arabisé ne l'a jamais mentionné ou utilisé, sauf pour le peuple arabophone d'Égypte. En tant que tel, il ne peut s’agir que d’une virgule égyptienne.

L'analyse des instruments égyptiens anciens est cohérente avec les multiples de la virgule égyptienne [voir les chapitres sous Les instruments de musique égyptiens, plus loin dans ce livre].

Nous mesurons les distances en pouces et en centimètres. Nous mesurons le poids en livres, grammes et kilogrammes. En musique, l'Occident au 19^ème siècle a décidé d'utiliser des unités standard pour mesurer les intervalles musicaux. Leur choix s'est porté sur le cent, où une octave = 1 200 cents.

Le système égyptien depuis ses débuts a utilisé le système musical virgule cela équivaut à 22,6415 cents et sa valeur d'un tiers de 7,55 cents l'appelle buk el-nunu, ce qui signifie le la bouche de bébé comme le rapportent les premiers écrivains grecs.

L’utilisation de ces incréments discrets « uniques » de la virgule égyptienne et du buk-nunu a été prouvée de manière cohérente dans tous les instruments égyptiens anciens.

Dans les distances entre les trous des instruments à vent.

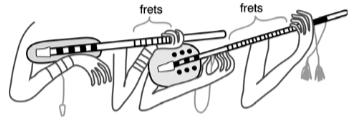
Dans les distances entre les frettes des instruments à cordes.

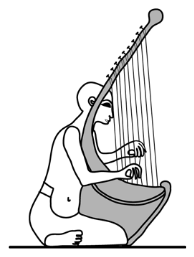
Dans les rapports entre les longueurs des cordes de harpe.

Chaque virgule égyptienne se compose de trois parties égales, que les Égyptiens appelaient/appelaient buk-nunu-c'est-à-dire le bouche du bébé. C'était/est un terme égyptien et non arabe (la bouche d'un bébé en arabe signifie Fam El Radee-a). Il est à noter que la division en tiers est cohérente avec la notion de Cinquième, puisque les 2/3 d'une virgule sont la Cinquième à l'intérieur de la virgule.

Les trois buk-nunu entre une virgule doivent être considérés comme le Trois-en-Un – le concept égyptien de la trinité [pour en savoir plus sur ce sujet, consultez Cosmologie égyptienne : l'univers animé, du même auteur].

La taille de buk-nunu est directement lié au calendrier égyptien antique très particulier, comme nous le verrons dans le prochain chapitre.