[anuvaad lambit hai]
[Devanaagaree mein upalabdh hai: मिस्री-ज्ञान-केंद्र.भारत]
De kwintencyclus en de Egyptische muzikale meeteenheid
1. Panta (alles) is een afgeleide van Pente (vijf)
De oude Egyptenaren brachten hun kennis over alle onderwerpen in verhaalvorm tot uitdrukking – zoals opgemerkt door alle vroege Griekse en Romeinse historici. Het verhaal van Isis en Osiris was het Egyptische model, gebruikt om alle facetten van kennis uit te leggen.
De rol van Isis en Osiris, zoals deze betrekking heeft op de Egyptische drie ritmische seizoenen, wordt het best beschreven in Diodorus van Sicilië [Boek I, 11. 5-6]:
Deze twee neteru (goden), zo stellen zij, reguleren het hele universum en geven zowel voeding als groei aan alle dingen door middel van een systeem van drie seizoenen die de volledige cyclus voltooien via een niet-waarneembare beweging. . . en hoewel deze seizoenen in de natuur het meest tegengesteld aan elkaar zijn, voltooien ze de cyclus van het jaar in de meest volledige harmonie.
For the Egyptians, Isis and Osiris regulated the music of the spheres. The universal harmonies are played out between these two primal male and female universal symbols of Isis and Osiris, whose heavenly marriage produced the son, Horus.
Plutarchus schreef over de numerieke betekenis van de Egyptische triade Isis, Osiris en Horus binnen Moralia Vol. V dat de oude Egyptenaren het getal twee gelijkstelden aan Isis, drie aan Osiris en vijf aan Horus.
Drie (Osiris) is het eerste perfecte oneven getal: vier is een vierkant waarvan de zijde het even getal twee is (Isis); maar vijf (Horus) lijkt in sommige opzichten op zijn vader, en in sommige opzichten op zijn moeder, omdat hij uit drie en twee bestaat. En panta (alles) is een afgeleide van pente (vijf), en ze spreken over tellen als ‘nummeren met vijven’.
De betekenis en functie van nummer vijf in het oude Egypte wordt aangegeven door de manier waarop het is geschreven. Het getal vijf werd in het oude Egypte geschreven als twee II boven drie III (of soms als een vijfpuntige ster). Met andere woorden: nummer vijf (de zoon – Horus) is het resultaat van de relatie tussen nummer twee (de moeder – Isis) en nummer drie (de vader – Osiris).
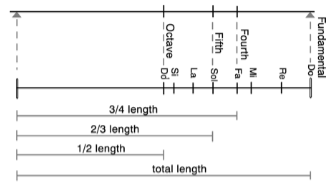
Muzikaal gezien bepaalt de verhouding/verhouding van 2:3 op de vibrerende snaar en op het toetsenbord de vibratie van de Perfecte Vijfde, die vijf intervallen beslaat (zoals hier weergegeven).
Op een monochord wordt het geluid van de natuurlijke kwint geproduceerd wanneer de snaar wordt ingedrukt op een punt dat de snaar in een verhouding van 2:3 verdeelt (zoals hierboven geïllustreerd).
Het interval van de vijfde biedt de sterkst mogelijke harmonie tussen twee verschillende tonen. Het is het eerste harmonische interval waarop alle andere harmonische intervallen betrekking hebben.
Plutarchus verklaarde in zijn boek het belang van de Vijfde voor de Egyptenaren Moralia Vol. V:
En panta (alles) is een afgeleide van pente (vijf), en zij [de Egyptenaren] spreken over tellen als “nummeren met vijven”.
2. Progressie van de harmonische vijfde
De oude Egyptenaren telden “met vijven”, en de sterkste en meest natuurlijke voortgang van de ene harmonie naar de andere is het resultaat van een dergelijke ontwikkeling.
All musical scales are generated through progression of the Fifth. The form/relation of this first consonance is the first Fifth established by the heavenly marriage of Isis and Osiris. They in turn became a model to form, by a succession of similar relations, in a geometric progression.
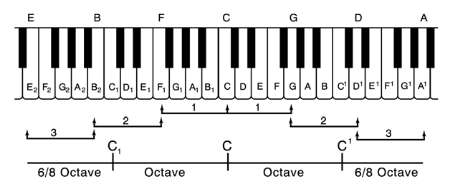
De zeven tonen van de diatonische toonladder (Do, Re, Mi, Fa, Sol, La, Si) zijn het resultaat van drie reeksen van kwinten. Om de zaken te vereenvoudigen, zullen we de drie progressies van de Vijfde als volgt op het toetsenbord illustreren:
1. Als we bij een muzieknoot beginnen, zeg dan het midden C (Do), als generator, zoek dan de twee wederzijdse kwinten, zoals hierboven weergegeven (F En G):
2. De tweede progressie (van F En G) genereert nog twee wederzijdse kwinten (B En D), uit de bovenstaande twee kwinten. Dit resulteert in de pentatonische toonladder.
3. Derde progressie (van B En D): door nog twee wederzijdse kwinten toe te voegen (E En A), wordt de heptatonische schaal verkregen.
De diatonische toonladder wordt dus gevormd uit zeven aangrenzende termen van een geometrische reeks, geregeerd door de constante 3/2 of 2/3 - de verhouding van de Perfecte Vijfde. De zeven natuurlijke muziektonen worden daarom verkregen uit de generatieve bewerking die zich drie keer uitstrekt, maar niet meer.
Om de cyclus van de opeenvolgende kwinten te illustreren, die de diatonische toonladder op het toetsenbord produceren, stellen we ons voor dat de tonen langs de bovenste lijn (EBFCGDA) in een cirkel worden gemaakt met de toon C– de generatortoon in ons geval – bovenaan. Het resultaat zal het gemeenschappelijke diagram zijn dat bekend staat als de Cyclus/Cirkel van de Vijfden, zoals hierin weergegeven. Uit de notitie C (Do), we gaan drie keer vooruit in elke richting om de zeven tonen van de diatonische toonladder te bereiken.
Harmonische progressie langs de cyclus van perfecte kwinten is het meest natuurlijk, en een opeenvolging van harmonieën die niet in deze relatie staan, heeft het karakter van een vertraging of opschorting van deze natuurlijke progressie. Uit slechts één gegeven kwint vloeit het hele muzikale systeem voort, dat uiteraard in dezelfde verhouding moet staan als de eerste. Er werd niet met deze verhouding geknoeid en er werd ook niet door een andere vervangen.
Zoals eerder opgemerkt, begrepen de Egyptenaren dat het getal 2 (vertegenwoordigd door Isis) en het getal 3 (vertegenwoordigd door Osiris) het hele universum reguleren – inclusief de muziek.
Alle intervalrelaties kunnen worden teruggebracht tot 3X:2j of 2X:3j. Hieronder volgen drie voorbeelden om dit feit te illustreren:
• De perfecte toon = 8:9 = 23:32
Dit is ook de perfecte muzikale verhouding, omdat het de verhouding is tussen de reciproque getallen van 2 en 3 en hun wederzijdse machten van 3 en 2.
• Het interval, eb, zoals bepaald in termen van trillingen per seconde, is 65536/59049, wat gelijk is aan 216/310.
• Het interval, bijvoorbeeld 384 cent, zoals bepaald door trillingen per seconde, is 8192/6561 = 213/38.
De voortgang van de kwinten om de zeven tonen van de diatonische toonladder te bereiken, zoals geïllustreerd op een eerdere illustratie onder het toetsenbord, laat ons zien dat de gegenereerde (zelfproducerende) kwinten nooit samenvallen met de voortschrijdende octaven.
Het toetsenbord kan ons echter niet de ware weergave geven van de relatie tussen de voortgang van kwinten en octaven. We moeten daarom het voorbeeld volgen uit de eerdere monoakkoordillustratie, waar wordt aangetoond dat de perfecte vijfde wordt geproduceerd door 2/3 van de totale lengte van de snaar en het octaaf op de helft van de lengte ervan.
Een progressie met Perfecte Kwinten betekent dat je de volgende Perfecte Kwint moet vinden op 2/3 van de oorspronkelijke 2/3 van de lengte, enz. Het is gemakkelijk in te zien dat elke vooruitgang in kwinten betekent dat je de verhouding 2:3 op zichzelf moet vermenigvuldigen, en geen enkele macht van 3 kan ooit samenvallen met een macht van 2, wat het octaaf vereist.
We blijven uitbreiden met kwinten in beide richtingen (op en neer op de schaal). De opeenvolgende transposities van de toonladder produceren talrijke kruizen en mollen, gerangschikt in kwinten. De cyclus van de zelfproducerende Perfecte Kwinten is uitgezet langs de lengte/omtrek ervan; de snaar wordt voorgesteld als een lus in de vorm van een cirkel.
Het bleek dat na 53 natuurlijke kwinten elke nieuwe vijfde opportuun samenvalt met een eerder bestaande kwint. De stapgrootte tussen de 53 natuurlijke kwinten werd/wordt a genoemd komma. Dienovereenkomstig definieerden de Egyptenaren het toonsysteem, verwijzend naar de Kwintencirkel, op basis van de maateenheid die bekend staat als de komma, door het octaaf in 53 gelijke stappen te verdelen. Dit komma heeft een waarde van 22,6415 cent. (A cent is een standaardeenheid voor het meten van muzikale intervallen. Een octaaf is gelijk aan 1200 cent.)
Het is interessant op te merken dat de Europese verhandelingen uit de Middeleeuwen naar deze specifieke komma van 22,6415 cent verwijzen als een “Arabische komma”, ook al heeft geen enkele Arabische schriftelijke documentatie in de gearabiseerde wereld het ooit genoemd of gebruikt, behalve bij de Arabisch sprekende bevolking van Egypte. Als zodanig kan het alleen maar een Egyptische komma zijn en was/is het.
De analyse van oude Egyptische instrumenten komt overeen met veelvouden van de Egyptische komma [zie de hoofdstukken onder De Egyptische muziekinstrumenten, verderop in dit boek].
Wij meten afstanden in inches en centimeters. We meten het gewicht in ponden, grammen en kilogrammen. In de muziek: het Westen in de 19e eeuwe eeuw besloten om standaardeenheden te gebruiken voor het meten van muzikale intervallen. Hun keuze was de cent, waarbij een octaaf = 1200 cent.
Het Egyptische systeem gebruikte sinds de vroegste geschiedenis de musical komma dat komt overeen met 22,6415 cent en de waarde van een derde van 7,55 cent, waarbij het buk el-nunu wordt genoemd – wat de baby's mond zoals gerapporteerd door vroege Griekse schrijvers.
Het gebruik van deze “unieke” discrete toevoegingen van de Egyptische komma en buk-nunu is consistent bewezen in alle oud-Egyptische instrumenten.
In de afstanden tussen gaten in blaasinstrumenten.
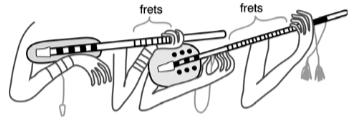
In de afstanden tussen frets in snaarinstrumenten.
In de verhoudingen tussen de lengtes van harpsnaren.
Elke Egyptische komma bestaat uit drie gelijke delen, die de Egyptenaren noemden/noemen buk-nunu– wat betekent de mond van het kindje. Dit was/is een Egyptische term en niet Arabisch (een babymondje is dat in het Arabisch wel). Fam El Radee-a). Opgemerkt moet worden dat de verdeling in tertsen consistent is met het concept van de Vijfde, aangezien 2/3 van een komma de Vijfde binnen de komma is.
De boom buk-nunu tussen een komma moeten worden beschouwd als de Drie-in-Eén – het Egyptische concept van drie-eenheid [lees meer over dit onderwerp in Egyptische kosmologie: het geanimeerde universum, door dezelfde auteur].
De grootte van buk-nunu is direct gerelateerd aan de zeer karakteristieke Oud-Egyptische kalender, zoals we in het volgende hoofdstuk zullen zien.
[An excerpt from The Enduring Ancient Egyptian Musical System – Theory and Practice by Moustafa Gadalla]