[anuvaad lambit hai]
[Devanaagaree mein upalabdh hai: मिस्री-ज्ञान-केंद्र.भारत]
The Cycle of Fifths And The Egyptian Musical Measuring Unit
1. Panta (All) Is A Derivative Of Pente (Five)
The Ancient Egyptians expressed their knowledge of all subjects in a story-form fashion—as noted by all early Greek and Roman historians. The story of Isis and Osiris was the Egyptian model, used to explain all facets of knowledge.
The role of Isis and Osiris, as it relates to the Egyptian three rhythmic seasons, is best described in Diodorus of Sicily [Book I, 11. 5-6]:
These two neteru (gods), they hold, regulate the entire universe, giving both nourishment and increase to all things by means of a system of three seasons which complete the full cycle through an unobservable movement. . . and these seasons, though in nature most opposed to one another, complete the cycle of the year in the fullest harmony.
For the Egyptians, Isis and Osiris regulated the music of the spheres. The universal harmonies are played out between these two primal male and female universal symbols of Isis and Osiris, whose heavenly marriage produced the son, Horus.
Plutarch wrote about the numerical significance of the Egyptian triad Isis, Osiris, and Horus in Moralia Vol. V that the Ancient Egyptians equated the number two to Isis, three to Osiris, and five to Horus.
Three (Osiris) is the first perfect odd number: four is a square whose side is the even number two (Isis); but five (Horus) is in some ways like to its father, and in some ways like to its mother, being made up of three and two. And panta (all) is a derivative of pente (five), and they speak of counting as “numbering by fives”.
The significance and function of number five, in Ancient Egypt, is indicated by the manner in which it was written. The number five in Ancient Egypt was written as two II above three III, (or sometimes as a five-pointed star). In other words, number five (the son–Horus) is the result of the relationship between number two (the mother–Isis) and number three (the father–Osiris).
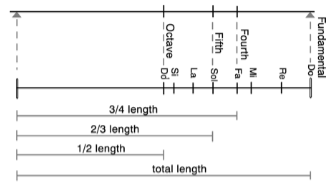
Musically, the ratio/relationship of 2:3 on the vibrating string and on the keyboard determines the vibration of the Perfect Fifth, reaching through five intervals (as shown here).
On a monochord, the sound of the natural Fifth is produced when the string is held down at a point that divides the string into a 2:3 ratio (as illustrated above).
The interval of the Fifth affords the strongest possible harmony between any two different tones. It is the first harmonic interval to which all other harmonic intervals relate.
Plutarch stated the importance of the Fifth for the Egyptians, in his Moralia Vol. V:
And panta (all) is a derivative of pente (five), and they [the Egyptians] speak of counting as “numbering by fives”.
2. Progression Of The Harmonic Fifth
The Ancient Egyptians counted “by fives”, and the strongest and most natural progression from one harmony to another is the result of such development.
All musical scales are generated through progression of the Fifth. The form/relation of this first consonance is the first Fifth established by the heavenly marriage of Isis and Osiris. They in turn became a model to form, by a succession of similar relations, in a geometric progression.
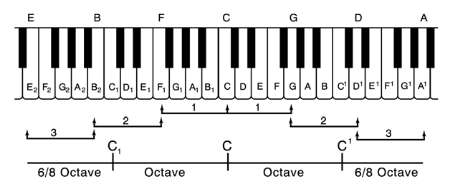
The seven tones of the diatonic scale (Do, Re, Mi, Fa, Sol, La, Si) are the result of three progressions of Fifths. To simplify matters, we will illustrate the three progression of the Fifth on the keyboard, as follows:
1. If we begin at any musical note, say the middle C (Do), as a generator, then find its two reciprocal Fifths, as shown above (F and G):
2. The second progression (from F and G) generates two more reciprocal Fifths (B and D), from the above two Fifths. This results in the pentatonic scale.
3. Third progression (from B and D): by adding two more reciprocal Fifths (E and A), the heptatonic scale is obtained.
The diatonic scale is thus formed from any seven adjacent terms of a geometric series, ruled by the constant 3/2 or 2/3—the proportion of the Perfect Fifth. The seven natural musical tones are therefore obtained from the generative operation that extend three times, but no more.
To illustrate the cycle of the consecutive Fifths, which produce the diatonic scale on the keyboard, we imagine that the tones along the top line (E B F C G D A) are made into a circle with the tone C—the generator tone in our case—at the top. The result will be the common diagram known as the Cycle/Circle of the Fifths, as shown herein. From the note C (Do), we progress three times in each direction, to reach the seven tones of the diatonic scale.
Harmonic progression along the cycle of Perfect Fifths is the most natural, and a succession of harmonies not in this relation has the character of a delay or suspension of this natural progression. From only one given Fifth flows the whole musical system, which naturally must be in the same proportion as the first. There was no tampering with this proportion and no substitution for another one.
As noted earlier, the Egyptians understood that the number 2 (represented by Isis) and the number 3 (represented by Osiris) regulate the entire universe—including music.
All interval relationships can be reduced to 3x:2y or 2x:3y. The following are three examples to illustrate such a fact:
• The Perfect Tone = 8:9 = 23:32
This is also the perfect musical ratio, because it is the ratio between the reciprocals of 2 and 3 to their reciprocal powers of 3 and 2.
• The interval, ebb, as determined in terms of vibrations per second, is 65536/59049, which equals 216/310.
• The interval, say 384 cents, as determined by vibrations per second, is 8192/6561 = 213/38.
The progression by the Fifths to reach the seven tones of the diatonic scale, as illustrated on an earlier illustration below the keyboard, shows us that the generated (self-producing) Fifths never coincide with the progressing octaves.
The keyboard, however, cannot give us the true representation of the relationship between the progression of fifths and octaves. We therefore must follow the example shown on the earlier mono-chord illustration where it is shown that the Perfect Fifth is produced by 2/3 of the total length of the string and the octave at ½ of its length.
A progression by Perfect Fifths will mean finding the next Perfect Fifth at 2/3 of the original 2/3 of the length, etc. It is easy to see that any progress in fifths means multiplying by the ratio 2:3 by itself, and no power of 3 can ever coincide with a power of 2, which the octave requires.
We continue expanding by the fifths in both directions (up and down the scale). The successive transpositions of the scale produce numerous sharps and flats, arranged by fifths. The cycle of the self-producing Perfect Fifths are plotted along its length/circumference—the string is imagined to be looped in the form of a circle.
It was found that after 53 natural Fifths, any new Fifth expediently coincides with a prior existing Fifth. The increment between the 53 natural Fifths was/is called a comma. Accordingly, the Egyptians defined the tone system, with reference to the Circle of Fifths, on the basis of the unit of measure known as the comma, by subdividing the octave into 53 equal steps. This comma has a value of 22.6415 cents. (A cent is a standard unit for measuring musical intervals. An octave is equal to 1200 cents.)
It is interesting to note that the European treatises of the Middle Ages refer to this particular comma of 22.6415 cents as an “Arabian Comma”, even though no Arabian written documentation in the Arabized world ever mentioned it or used it except for the Arabic-speaking people of Egypt. As such, it can only be and was/is an Egyptian comma.
Analysis of Ancient Egyptian instruments is consistent with multiples of the Egyptian comma [see chapters under The Egyptian Musical Instruments, later on in this book].
We measure distances in inches and centimeters. We measure weight in pounds, grams, and kilograms. In music, the West in the 19th century decided on using standard units for measuring musical intervals. Their choice was the cent—where an octave = 1,200 cents.
The Egyptian system since its earliest history used the musical comma that is equivalent to 22.6415 cents and its one third value of 7.55 cents calling it buk el-nunu—meaning the baby’s mouth as reported by early Greek writers.
The use of these “unique” discreet increments of the Egyptian comma and buk-nunu has been proven with consistency in all Ancient Egyptian instruments.
In the distances between holes in wind instruments.
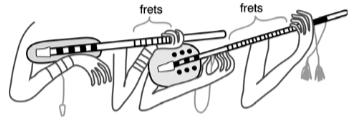
In the distances between frets in string instruments.
In the ratios between the lengths of harp strings.
Each Egyptian comma consists of three equal parts, which the Egyptians called/call buk-nunu—meaning the mouth of the baby. This was/is an Egyptian term and not Arabic (a baby’s mouth in Arabic is Fam El Radee-a). It should be noted that the division into thirds is consistent with the concept of the Fifth, since 2/3 of a comma is the Fifth within the comma.
The three buk-nunu in a comma are to be considered the Three-in-One—the Egyptian concept of trinity [read more about this subject in Egyptian Cosmology: The Animated Universe, by the same author].
The size of buk-nunu is directly related to the very distinctive Ancient Egyptian calendar, as we will see in the next chapter.
[An excerpt from The Enduring Ancient Egyptian Musical System – Theory and Practice by Moustafa Gadalla]