Géométrie sacrée et sciences naturelles

 

Pour les Égyptiens de l’Antiquité, la géométrie était bien plus qu’une étude de points, de lignes, de surfaces et de solides ; et leurs propriétés et mesures. L’harmonie héritée de la géométrie était reconnue dans l’Égypte ancienne comme l’expression la plus convaincante d’un plan divin qui sous-tend le monde – un plan métaphysique qui détermine le physique.

Pour les anciens Égyptiens, la géométrie était le moyen par lequel l’humanité pouvait comprendre les mystères de l’ordre divin. La géométrie existe partout dans la nature : son ordre sous-tend la structure de toutes choses, des molécules aux galaxies. La nature de la forme géométrique permet son fonctionnement. La conception, utilisant les principes de la géométrie sacrée, doit atteindre le même objectif ; c'est-à-dire un formulaire pour servir/représenter une fonction.

La géométrie sacrée traite non seulement des proportions des figures géométriques, mais aussi des relations harmonieuses des parties avec le tout, comme les parties de l'être humain dans leurs relations les unes avec les autres, la structure des plantes et des animaux et les formes. de cristaux et d’objets naturels, qui sont tous des manifestations du continuum universel.

La clé de la proportion harmonique divine (géométrie sacrée) est la relation entre la progression de la croissance et la proportion. La proportion harmonique et la progression sont l'essence de l'univers créé. Cela correspond à la nature qui nous entoure. La nature qui nous entoure suit cette relation harmonieuse. La progression naturelle suit une série popularisée en Occident sous le nom de « série Fibonacci ».

Puisque cette série existait avant Fibonacci (né en 1179 CE), elle ne devrait pas porter son nom. Fibonacci lui-même et ses commentateurs occidentaux n’ont même pas affirmé qu’il s’agissait de sa « création ». Appelons-le tel qu'il est : un Série de synthèse. Il s'agit d'une série progressive dans laquelle vous commencez par les deux premiers nombres du système égyptien antique, c'est-à-dire 2 et 3. Ensuite, vous ajoutez leur total au nombre précédent, et ainsi de suite. Tout chiffre est la somme des deux précédents. La série serait donc : 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, etc.

Cette série se reflète dans toute la nature. Le nombre de graines d’un tournesol, les pétales de n’importe quelle fleur, la disposition des pommes de pin, la croissance d’une coquille de nautile, etc. – suivent tous le même schéma de ces séries.

Des preuves accablantes indiquent que la série Sommation était connue des anciens Égyptiens. Les plans égyptiens antiques des temples et des tombeaux, tout au long de sa longue histoire, montrent que les éléments majeurs des temples sont positionnés le long de leur axe longitudinal, suivant les numéros consécutifs de la série de sommation (2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, etc.).

Une fois que les dimensions des monuments égyptiens antiques sont indiquées dans les unités égyptiennes antiques de la coudée (1,72 pi/0,528 m), il devient clair que la série Summation est une idée originale des anciens Egyptiens. La série de sommations est parfaitement conforme et peut être considérée comme une expression des mathématiques égyptiennes, qui ont été définies par chacun comme une théorie essentiellement procédure additive.

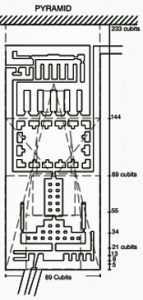
Il existe des preuves de la connaissance de la série de sommation depuis le temple pyramidal (appelé à tort morgue) de Khafra (Chephren) à Gizeh, construit en 2500 avant notre ère (environ 3 700 ans avant Fibonacci).

Les points essentiels du temple [montrés ici] sont conformes à la série de sommation, qui atteint le chiffre de 233 coudées dans sa longueur totale, mesurée à partir de la pyramide, avec DIX nombres consécutifs de la série.

Concernant l'application étroite actuelle du terme « géométrie », tous les aspects de notre géométrie moderne ont été perfectionnés dans l'Égypte ancienne il y a longtemps. Leurs connaissances avancées sont clairement évidentes dans quelques papyrus récupérés, communément appelés papyrus « mathématiques » de l’Égypte ancienne. Plus de détails concernant ces papyrus seront fournis ultérieurement.

 

[Un extrait de Égyptien ancien : la culture révélée, deuxième édition par Moustafa Gadalla]
https://egyptianwisdomcenter.org/product/la-culture-de-legypte-ancienne-revelee/

https://egyptianwisdomcenter.org/product/la-culture-de-legypte-ancienne-revelee/