Sacred Geometry And Natural Sciences

 

Geometry, to the Ancient Egyptians, was much more than a study of points, lines, surfaces, and solids; and their properties and measurement. The harmony inherit in geometry was recognized in Ancient Egypt as the most cogent expression of a divine plan that underlies the world—a metaphysical plan that determines the physical.

For the Ancient Egyptians, geometry was the means by which humanity could understand the mysteries of the divine order. Geometry exists everywhere in nature: its order underlies the structure of all things, from molecules to galaxies. The nature of the geometric form allows its functioning. The design, using the principles of sacred geometry, must achieve the same goal; i.e. form to serve/represent a function.

Sacred geometry deals not only with the proportions of geometrical figures, but also with the harmonic relations of the parts to the whole, such as the parts of the human being as they relate to one another, the structure of plants and animals, and the forms of crystals and natural objects—all of which are manifestations of the universal continuum.

The key to divine harmonic proportion (sacred geometry) is the relationship between the progression of growth and proportion. Harmonic proportion and progression are the essence of the created universe. It is consistent with nature around us. Nature around us follows this harmonious relationship. The natural progression follows a series that is popularized in the West as the “Fibonacci Series”.

Since this Series was in existence before Fibonacci (born in 1179 CE), it should not bear his name. Fibonacci himself and his Western commentators did not even claim that it was his “creation”. Let us call it as it is—a Summation Series. It is a progressive series, where you start with the first two numbers in the Ancient Egyptian system – i.e. 2 and 3. Then you add their total to the preceding number, and on and on. Any figure is the sum of the two preceding ones. The series would therefore be: 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, etc.

This series is reflected throughout nature. The number of seeds in a sunflower, the petals of any flower, the arrangement of pine cones, the growth of a nautilus shell, etc. – all follow the same pattern of these series.

Overwhelming evidence indicates that the Summation Series was known to the Ancient Egyptians. The Ancient Egyptian plans of temples and tombs, throughout its long history, show that the major elements of the temples are positioned along their longitudinal axis, following the consecutive numbers of the Summation Series (2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, etc.).

Once the dimensions of the Ancient Egyptian monuments are shown in the Ancient Egyptian units of the cubit (1.72 ft./0.528 m), it becomes crystal clear that the Summation Series is the brainchild of the Ancient Egyptians. The Summation Series conforms perfectly with and can be regarded as an expression of Egyptian mathematics, which has been defined by everyone as an essentially additive procedure.

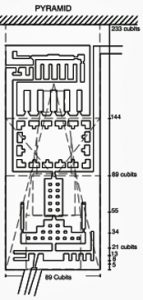
There is evidence about the knowledge of the Summation Series ever since the Pyramid (erroneously known as mortuary) Temple of Khafra (Chephren) at Giza, built in 2500 BCE (about 3,700 years before Fibonacci).

The essential points of the temple [shown herein] comply with the Summation Series, which reaches the figure of 233 cubits in its total length, as measured from the pyramid, with TEN consecutive numbers of the series.

Regarding the present-day narrow application of the term ‘geometry’, all aspects of our modern geometry were perfected in Ancient Egypt a long time ago. Their advanced knowledge is clearly evident in a few recovered papyri which are commonly known as the Ancient Egyptian “mathematical” papyri. More details regarding these papyri will be provided later.

 

[An excerpt from Ancient Egyptian: Culture Revealed, Second Edition by Moustafa Gadalla]
https://egyptianwisdomcenter.org/product/ancient-egyptian-culture-revealed-second-edition/

https://egyptianwisdomcenter.org/product/ancient-egyptian-culture-revealed-second-edition/